侧面积和全面积的定义:
(1)侧面积的定义:把柱、锥、台的侧面沿着它们的一条侧棱或母线剪开,所得到的展开图的面积,就是空间几何体的侧面积.
(2)全面积的定义:空间几何体的侧面积与底面积的和叫做空间几何体的全面积,
柱体、锥体、台体的表面积公式(c为底面周长,h为高,h′为斜高,l为母线)
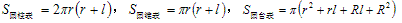
柱体、锥体、台体的体积公式:
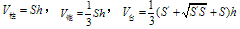
多面体的侧面积与体积:
| 多面体 | 图像 | 侧面积 | 体积 |
| 棱柱 |  | 直棱柱的侧面展开图是矩形 |  |
| 棱锥 |  | 正棱柱的侧面展开图是一些全等的等腰三角形, |  |
| 棱台 |  | 正棱台的侧面展开图是一些全等的等腰梯形,  |  |
旋转体的侧面积和体积:
| 旋转体 | 图形 | 侧面积与全面积 | 体积 |
| 圆柱 |  | 圆柱的侧面展开图的矩形: |  |
| 圆锥 |  | 圆锥的侧面展开图是扇形: |  |
| 圆台 |  | 圆台的侧面展开图是扇环: |  |
| 球 |  |  |  |
相关高中数学知识点:球的表面积与体积
球的体积公式:
V球=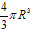 ;
;
球的表面积:
S球面=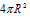
求球的表面积和体积的关键:
由球的表面积和体积公式可知,求球的表面积和体积的关键是求出半径。
常用结论:
1.若球的表面积变为原来的2倍,则半径变为原来的 倍.
倍.
2.若球半径变为原来的2倍,则表面积变为原来的4倍.
3.若两球表面积之比为1:2,则其体积之比是 .
.
4.若两球体积之比是1:2,则其表面积之比是 .
.
相关高中数学知识点:组合体的表面积与体积
定义:
组合体的表面积与体积主要通过计算组成几何体的简单几何体的表面积与体积来求解。
组合体的表面积和体积与球有关的组合体问题:
一种是内切,一种是外接.解题时要认真分析图形,明确切点和接点的位置,确定有关元素间的数量关系,并作出合适的截面图.如球内切于正方体,切点为正方体各个面的中心,正方体的棱长等于球的直径;球外接于正方体,正方体的顶点均在球面上,正方体的体对角线长等于球的直径.球与旋转体的组合,通常作它们的轴截面解题,球与多面体的组合,通过多面体的一条侧棱和球心,或”、点。
求几何体的体积的几种常用方法:
(1)分割求和法:把不规则的图形分割成规则的图形,然后进行体积求和;
(2)补形法:把不规则形体补成规则形体,不熟悉形体补成熟悉形体,便于计算其体积;
常见的补形方法:


(3)等体积转化法:从不同的角度看待原几何体,通过改变顶点和底面,利用体积不变的原理,求原几何体的体积。
本文来自:逍遥右脑记忆 /gaozhong/885888.html
相关阅读:高考数学复习:系统梳理 重点掌握
高中数学学习方法:高二数学复习八大原则
科学把握数学新课标
高中数学:扇形的面积公式_高中数学公式
三角函数图象性质
