数列的极限定义（描述性的）：

如果当项数n无限增大时，无穷数列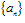的项a_n无限地趋近于某个常数a（即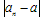无限地接近于0），a叫数列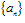的极限，记作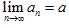，也可记做当n→+∞时，a_n→a。

数列的极限严格定义：

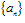即ε－N定义：对于任何正数ε（不论它多么小），总存在某正数N，使得当n＞N时，一切a_n都满足，a叫数列的极限。

数列极限的四则运算法则：

若，则
（1），；
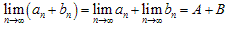（2），；
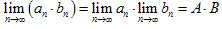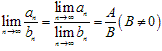（3）。
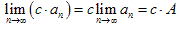前提条件：（1）各数列均有极限，（2）相加减时必须是有限个数列才能用法则。

a_n无限接近于a的方式有三种：

第一种是递增的数列，a_n无限接近于a，即a_n是在常数a的左边无限地趋近于a，如n→+∞时，；
第二种是递减数列，a_n无限地趋近于a，即a_n是在常数a的右边无限地趋近于a，如n→+∞时，是；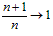
第三种是摆动数列，a_n无限地趋近于a，即a_n是在无限摆动的过程中无限地趋近于a，如n→+∞时，。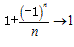

一些常用数列的极限：

（1）常数列A，A，A，…的极限是A；
（2）当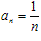时，；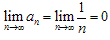
（3）当|q|＜1时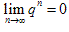，；当q＞1时，不存在；
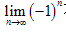（4）不存在，。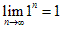
（5）无穷等比数列{a_n}中，首项a₁，公比q，前n项和S_n，各项之和S，则（只有在0＜|q|＜1时）。

本文来自：逍遥右脑记忆 /gaozhong/854115.html

相关阅读：高中数学学习方法：高二数学复习八大原则
高考数学复习：系统梳理 重点掌握
科学把握数学新课标
三角函数图象性质
高中数学：扇形的面积公式_高中数学公式