抛物线的参数方程：

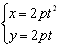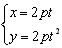如图，抛物线y²=2px（p＞0）（或x²=2py（p＞0））的参数方程为（或）（t为参数，t∈R）。

几何意义为：

t表示抛物线上除顶点外的任意一点与原点连线的斜率的倒数。即M（x,y）为抛物线上任意一点，则有

抛物线的参数方程的推导：


设抛物线的普通方程为
因为点M在α的终边上,根据三角函数的定义可得
由(5)(6)解出x,y，得到
这就是抛物线（5）（不包括顶点）的参数方程。
如果令 则有
当t=0时，由参数方程表示的点正好就是抛物线的顶点（0，0），因此时，参数方程就表示抛物线。

本文来自：逍遥右脑记忆 /gaozhong/807347.html

相关阅读：高中数学学习方法：高二数学复习八大原则
科学把握数学新课标
高考数学复习：系统梳理 重点掌握
三角函数图象性质
高中数学：扇形的面积公式_高中数学公式