指数函数的定义：

一般地，函数y=a^x（a＞0，且a≠1）叫做指数函数，其中x是自变量，函数的定义域是R，值域是（0，+∞）。

指数函数的解析式：

y=a^x（a＞0，且a≠1）

理解指数函数定义，需注意的几个问题：

①因为a>0，x是任意一个实数时，a^x是一个确定的实数，所以函数的定义域为实数集R．
②规定底数a大于零且不等于1的理由：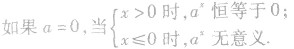

如果a<0，比如y=(-4)^x，这时对于在实数范围内函数值不存在．
如果a=1，y=1^x=1是一个常量，对它就没有研究的必要，
为了避免上述各种情况，所以规定a>0且a≠1．
③像等函数都不是指数函数，要注意区分。

相关高中数学知识点：指数与指数幂的运算（整数、有理、无理）

n次方根的定义：

一般地，如果xⁿ=a，那么x叫做a的n次方根，其中n＞1，且n∈N*。

分数指数幂的意义：

（1）；
（2）；
（3）0的正分数指数幂等于0，0的负分数指数幂没有意义。

n次方根的性质：

（1）0的n次方根是0，即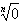＝0（n＞1，n∈N*）；
（2）=a（n∈N*）；
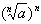（3）当n为奇数时，=a；当n为偶数时，＝|a|。

幂的运算性质：

（1）；
（2）；
（3）；
注意：一般地，无理数指数幂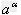（a＞0，α是无理数）是一个确定的实数，上述有理指数幂的运算性质，对于无理指数幂都适用。

本文来自：逍遥右脑记忆 /gaozhong/590356.html

相关阅读：高考数学复习：系统梳理 重点掌握
高中数学：扇形的面积公式_高中数学公式
三角函数图象性质
科学把握数学新课标
高中数学学习方法：高二数学复习八大原则