分类变量与列联表：

变量的不同“值”表示个体所属的不同类别，像这类变量称为分类变量；
列出的两个分类变量的频数表，称为列联表。

独立性检验：

为了使不同样本容量的数据有统一的评判标准，构造一个随机变量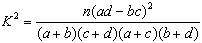，其中n=a+b+c+d为样本容量。利用随机变量K²来确定在多大程度上可以认为“两个分类变量有关系”的方法，称为两个分类变量的独立性检验。

利用独立性检验来考察两个分类变量是否有关系，并且能较精确地给出这种判断的可靠程度，具体做法是：

（1）根据实际问题需要的可信程度确定临界值k₀；
（2）利用公式（1），由观测数据计算得到随机变量K²的观测值；
（3）如果k＞k₀，就以（1-P（K²≥k₀））×100%的把握认为“X与Y有关系”；否则就说样本观测数据没有提供“X与Y有关系”的充分证据。

独立性检验的性质：

独立性检验没有直观性，必须依靠K² 的观测值k作判断。

独立性检验的一般步骤：

（1）根据样本数据制成2×2列联表；
（2）根据公式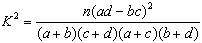，计算K²的值；
（3）查表比较K²与临界值的大小关系，作统计判断。

本文来自：逍遥右脑记忆 /gaozhong/460053.html

相关阅读：高中数学：扇形的面积公式_高中数学公式
科学把握数学新课标
三角函数图象性质
高考数学复习：系统梳理 重点掌握
高中数学学习方法：高二数学复习八大原则