圆的定义：

平面内与一定点的距离等于定长的点的集合是圆。定点就是圆心，定长就是半径。

圆的标准方程：

圆的标准方程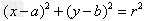，圆心（a，b），半径为r；特别当圆心是（0，0），半径为r时，圆的标准方程为。

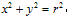圆的一般方程：

圆的一般方程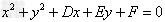
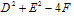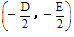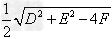当＞0时，表示圆心在，半径为的圆；
当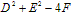=0时，表示点；
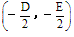当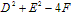＜0时，不表示任何图形。

圆的定义的理解：

（1）定位条件：圆心；定形条件：半径。
（2）当圆心位置与半径大小确定后，圆就唯一确定了．因此一个圆最基本的要素是圆心和半径．

圆的方程的理解：

(1)圆的标准方程中含有a，b，r三个独立的系数，因此，确定一个圆需三个独立的条件．其中圆心是圆的定位条件，半径是圆的定形条件．
(2)圆的标准方程的优点在于明确显示了圆心和半径．
(3)圆的一般方程形式的特点：
a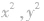．的系数相同且不等于零；
b．不含xy项．
(4)形如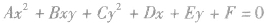的方程表示圆的条件：
a．A=C≠0；
b．B=0;
c.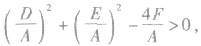即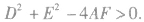

几种特殊位置的圆的方程：

条件	标准方程	一般方程
圆心在原点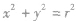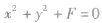
过原点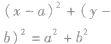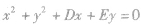
圆心在x轴上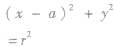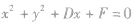
圆心在y轴上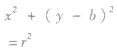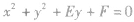
与x轴相切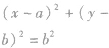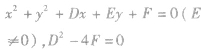
与y轴相切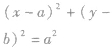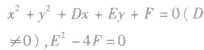
与x,y轴都相切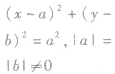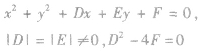
圆心在x轴上且过原点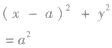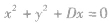
圆心在y轴上且过原点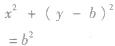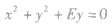

本文来自：逍遥右脑记忆 /gaozhong/437397.html

相关阅读：高中数学学习方法：高二数学复习八大原则
高考数学复习：系统梳理 重点掌握
三角函数图象性质
科学把握数学新课标
高中数学：扇形的面积公式_高中数学公式