面面平行的定义：

如果两个平面无公共点，则称这两个平面平行。

图形表示：

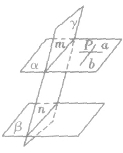
面面平行的判定定理：

（1）如果一个平面内的两条相交直线与另一个平面平行，那么这两个平面平行； （线面平行面面平行），
（2）如果一个平面内有两条相交直线分别平行于另一平面内的两条直线，那么这两个平面平行。（线线平行面面平行），
（3）垂直于同一条直线的两个平面平行。
（4）平行于同一个平面的两个平面平行。

符号语言：
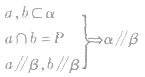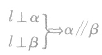（1） ；（3） ；（4）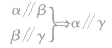

面面平行的性质定理：

（1）如果两个平行平面同时与第三个平面相交，那么它们的交线平行。 （面面平行线线平行）
（2）如果两个平面平行，那么某一个平面内的直线与另一个平面平行。 （面面平行线面平行）
（3）如果两个平行平面中有一个平面垂直于一条直线，那么另一个平面也垂直于这条直线。

符号语言：
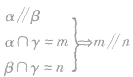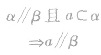（1） ；（2） ；（3）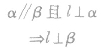

线线平行、线面平行、面面平行间的关系：

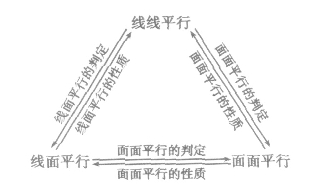
由于三者之间相互沟通、相互联系，因此立体几何问题的解决往往一题多解（证）。

证明面面平行的常用方法：

(1)反证法，即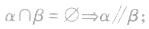
(2)判定定理或推论，即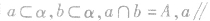
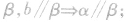
(3)“垂直于同一直线的两个平面平行”这一性质，即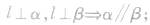
(4)向量法，两个平面的法向量平行，则这两个平面平行。

本文来自：逍遥右脑记忆 /gaozhong/326159.html

相关阅读：三角函数图象性质
高中数学学习方法：高二数学复习八大原则
高考数学复习：系统梳理 重点掌握
高中数学：扇形的面积公式_高中数学公式
科学把握数学新课标