等比数列的定义：

一般地，如果一个数列从第2项起，每一项与它的前一项的比等于同一个常数，那么这个数列就叫做等比数列，这个常数叫做公比，公比通常用字母q表示（q≠0）。

等比数列的性质：

在等比数列｛a_n｝中，有
（1）若m+n=p+q，m，n，p，q∈N*，则a_ma_n=a_pa_q；当m+n=2p时，a_ma_n=a_p²；
（2）若m，n∈N*，则a_m=a_nq^m-n；
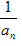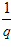（3）若公比为q，则｛｝是以为公比的等比数列；
（4）下标成等差数列的项构成等比数列；
（5）
1）若a₁＞0，q＞1，则｛a_n｝为递增数列；
2）a₁＜0，q＞1， 则｛a_n｝为递减数列；
3）a₁＞0，0＜q＜1，则｛a_n｝为递减数列；
4）a₁＜0， 0＜q＜1， 则｛a_n｝为递增数列；
5）q＜0，则｛a_n｝为摆动数列；若q＝1，则｛a_n｝为常数列。

等差数列和等比数列的比较：

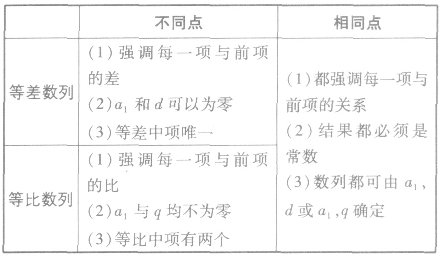
如何证明一个数列是等比数列：

证明一个数列是等比数列，只需证明是一个与n无关的常数即可（或a_n²=a_n-1a_n+1）。

本文来自：逍遥右脑记忆 /gaozhong/297113.html

相关阅读：高考数学复习：系统梳理 重点掌握
科学把握数学新课标
三角函数图象性质
高中数学：扇形的面积公式_高中数学公式
高中数学学习方法：高二数学复习八大原则