圆的切线方程:
1、已知圆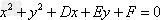 ,
,
(1)若已知切点 在圆上,则切线只有一条,其方程是
在圆上,则切线只有一条,其方程是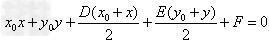 ;
;
(2)当 圆外时,
圆外时,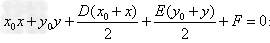 表示过两个切点的切点弦方程。
表示过两个切点的切点弦方程。
(3)过圆外一点的切线方程可设为 ,再利用相切条件求k,这时必有两条切线。
,再利用相切条件求k,这时必有两条切线。
(4)斜率为k的切线方程可设为y=kx+b,再利用相切条件求b,必有两条切线。
2、已知圆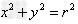 ,
,
(1)过圆上的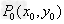 点的切线方程为
点的切线方程为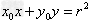 ;
;
(2)斜率为k的圆的切线方程为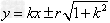 。
。
圆的切线方程的求法:
①代数法:设出切线方程,利用切线与圆仅有一个交点,将直线方程代入圆的方程,从而△=0,可求解;
②几何法利用几何特征:圆心到切线的距离等于圆的半径,可求解.
过定点的圆的切线方程:
①过圆上一点的切线方程:
与圆 的切线方程是
的切线方程是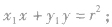
与圆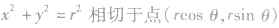 的切线方程是
的切线方程是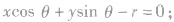
与圆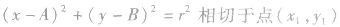 的切线方程是
的切线方程是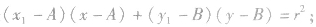
与圆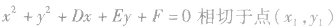 的切线方程是
的切线方程是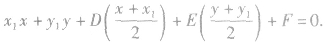
②过圆外一点的切线方程:设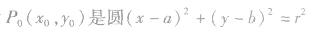 外一点,求过P0点的圆的切线.
外一点,求过P0点的圆的切线.
方法l:设切点是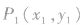 ,解方程组
,解方程组
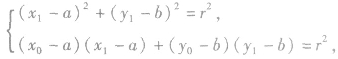 求出切点P1的坐标,即可写出切线方程。
求出切点P1的坐标,即可写出切线方程。方法2:设切线方程是
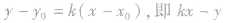
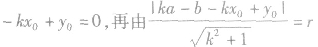 ,再由
,再由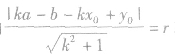 求出待定系数k,就可写出切线方程.
求出待定系数k,就可写出切线方程.特别提醒:一般说来,方法2比较简便,但应注意,可能遗漏k不存在的切线.因此,当解出的k值唯一时,应观察图形,看是否有垂直于x轴的切线.
本文来自:逍遥右脑记忆 /gaozhong/282837.html
相关阅读:科学把握数学新课标
高中数学学习方法:高二数学复习八大原则
三角函数图象性质
高中数学:扇形的面积公式_高中数学公式
高考数学复习:系统梳理 重点掌握
