异面直线所成角：

，
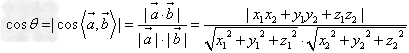（其中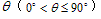为异面直线a，b所成角，分别表示异面直线a，b的方向向量）。

直线AB与平面所成角：

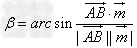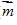（为平面α的法向量）；

二面角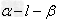的平面角：

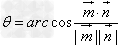或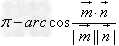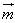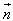（，为平面α，β的法向量）。

用向量求异面直线所成角注意：

①求异面直线所成的角常用平移法或向量法，特别是向量法，由于降低了空间想象的要求，所以需引起我们的重视，用向量法时，需注意两异面直线夹角的范围是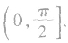
②两异面直线所成的角可以通过这两条直线的方向向量的夹角来求得，但二者不完全相等，当两方向向量的夹角是钝角时，应取其补角作为两异面直线所成的角．

求直线与平面所成的角既可选择传统立体几何的综合推理法，也可选择空间向量的向量法：

①求直线和平面所成角的步骤：作出斜线与其射影所成的角；证明所作的角就是要求的角；常在直角三角形（垂线、斜线、射影所组成的直角三角形）中解出所求角的大小：
②在用向量法求直线OP与α所成的角时一般有两种途径：一是直接求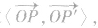其中OP′，为斜线OP在平面α内的射影；二是通过求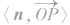进而转化求解，其中n为平面α的法向量。

用向量求二面角注意：

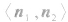①当法向量的方向分别指向二面角的内侧与外侧时，二面角θ的大小等于法向量的夹角的大小；
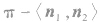②当法向量的方向同时指向二面角的内侧或外侧时，二面角θ的大小等于法向量的夹角的补角的大小．

求二面角，大致有两种基本方法：

(1)传统立体几何的综合推理法：①定义法；②垂面法；③三垂线定理法；④射影面积法．
(2)空间向量的坐标法：建系并确定点及向量的坐标，分别求出两个平面的法向量，通过求两个法向量的夹角得出二面角的大小．

本文来自：逍遥右脑记忆 /gaozhong/274655.html

相关阅读：高中数学：扇形的面积公式_高中数学公式
科学把握数学新课标
三角函数图象性质
高中数学学习方法：高二数学复习八大原则
高考数学复习：系统梳理 重点掌握